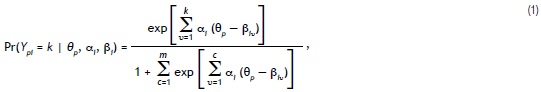
Anexo 1 Análisis TRI

Modelo. Se describe la extensión del modelo de crédito parcial generalizado (GPCM) para tomar en cuenta dependencias locales entre los ítems. El GPCM original¹⁶ es un modelo para la probabilidad de que una persona p, al contestar un ítem politómico i con m + 1 opciones de respuesta graduadas (con valores 0.. .m), responda en la categoría k (0 ≤ k ≤ m). Dicha probabilidad se da por:

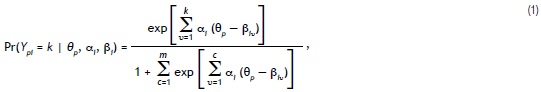
donde Y_pi es la variable aleatoria asociada con la respuesta de la persona p en el ítem i, θ_ρ es el nivel de la persona p en el constructo bajo consideración, α. es el grado de discriminación del ítem i y β_i = (β_i1.....ß_im) es un vector que contiene los grados de dificultad asociados con los respectivos umbrales del ítem i (que se definen por los pares de categorías de respuesta adyacentes). Nótese que, en el caso de k = 0, se define que la suma en el nominador iguala a 0.

Al considerar la probabilidad conjunta de dos o más respuestas de la misma persona, el GPCM original asume independencia local entre los ítems. Para dos ítems i e i', esto implica:

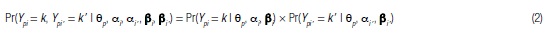
para 0 ≤ k, k' ≤ m.

En su artículo de 1997, Hoskens y De Boeck¹⁸ propusieron un marco teórico que organiza posibles causas por las que se invalide el supuesto de independencia local en modelos TRI y describieron cómo se puede adaptar el modelo para tomarlas en cuenta. Para la aplicación en este artículo, es importante mencionar el tipo de dependencia local que denominaron combinación constante, lo cual aplica especialmente en el caso de contenido compartido, es decir, cuando dos o más ítems de la escala hacen referencia a un subtema particular.

Aunque Hoskens y De Boeck elaboraron su método para el caso especial del modelo de Rasch, la aplicación de sus ideas al GPCM es bastante directa. Para simplificar la notación, escribiremos Pr(k, k' | θ_p) en vez de Pr(Y_pi = k, Y_pi׳ = k' | θ_p, α_i1, α_i', β_i β_i'). Hoskens y De Boeck consideran

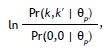
lo cual es un logaritmo de momios, comparando la probabilidad del patrón de respuestas (k, k') con el patrón (0,0). En el caso de independencia local, se puede derivar de las Ecuaciones (1) y (2):

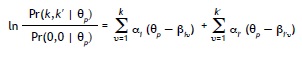
Para modelar dependencia local del tipo combinación constante en los ítems i e i', que en nuestros datos tienen cuatro categorías de respuesta, introducimos dos nuevos parámetros: β_ii'^(L) y β_ii'^(H). El primer parámetro entra en la ecuación si ambas respuestas caen en una de las dos categorías más altas (es decir, k,k' ≥ 2), el segundo si ambas respuestas caen en la categoría más alta (es decir, k = k' = 3). En específico, se distinguen los siguientes tres casos: (a) si k < 2 o k' < 2, entonces:

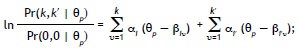
(b) si k > 2 o k > 2 y no k = k = 3, entonces:

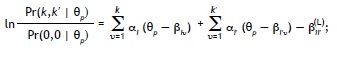
(c) si k = k' = 3, entonces:

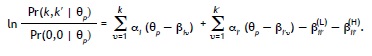
Los valores negativos para el parámetro β_ii'^(L) aumentan la probabilidad de que la persona conteste en ambos ítems "familiarizado" o "muy familiarizado" (en comparación con el GPCM original). Los valores positivos reducirían dicha probabilidad. El parámetro β_ii'^(H) tiene un efecto adicional y similar a la probabilidad de que la persona conteste en ambos ítems "muy familiarizado". En los resultados se obtuvieron valores negativos para ambos parámetros en el análisis de todas las escalas. Es posible extender el modelo más, según las mismas líneas, para incorporar interacciones de orden superior. No obstante, para el presente estudio consideramos únicamente interacciones por pares entre los ítems; es decir, aunque son tres o más ítems de la escala que se refieren a un mismo subtema, el modelo solo incluye la interacción entre cada par de estos ítems.

Estimación. Se estimó el modelo en un marco bayesiano, considerando la distribución posterior de los parámetros, condicional a los datos. El teorema de Bayes relaciona la distribución posterior con la función de verosimilitud y la distribución previa:

donde α es un vector con los grados de discriminación de todos los ítems, β un vector con los umbrales de todos los ítems y los parámetros de interacción (dependencia local), θ el vector de parámetros de todas las personas y y representa los datos observados.

La función de verosimilitud para el modelo se describió en los párrafos anteriores; para la distribución previa especificamos que cada parámetro fuera independientemente extraída de la siguiente forma:

Se implementó un algoritmo de Metropolis^23,24 con el fin de obtener una muestra de la distribución posterior. Se corrió el algoritmo con cuatro cadenas de Markov, inicializados con valores extraidos aleatoriamente de la distribución previa. Después de 5,000,000 iteraciones, se evaluó la convergencia de las cadenas a través del estadístico de Gelman y Rubin³⁸ calculado sobre la última mitad de las cadenas; en todos los análisis, se obtuvo < 1.20 para cada parámetro. Evaluación. Se evaluó la bondad de ajuste de cada ítem a través de comprobaciones predictivas posteriores (PPCs).¹⁷ Se utilizó como medida de discrepancia:

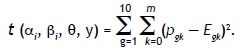
Para calcular el valor en t, se divide el grupo total de personas en 10 subgrupos de igual tamaño, con base en θ; p_gk es la proporción de personas en el grupo g que da la respuesta k al ítem i y E_gk es la probabilidad, bajo el GPCM, de que una persona con θ igual a la media del grupo g responda en la categoría k. Si el ítem i no se incluye en un grupo de ítems con dependencia local, E_gk se calcula a partir de la Ecuación (1); en el caso de que el ítem sí se afecte por la dependencia local con otros ítems, E_gk se obtiene considerando todos los patrones de respuesta en los ítems en el grupo y calculando la probabilidad marginal de la respuesta k en el ítem i a través de la suma de las probabilidades entre todas las categorías de respuesta del (los) otro(s) ítem(s).